O Programa de Pós-Graduação em Ciência, Tecnologia e Inovação (PPgCTI) está com processo seletivo aberto para bolsistas e voluntários dos…
A Escola de Ciências e Tecnologia (ECT) oferece, no período de 17 de abril a 07 de julho, o minicurso Introdução ao Cálculo Variacional. As aulas acontecem às terças e quintas-feiras, das 16h50 às 18h30 ou às segundas e quintas-feiras, das 14h55 às 16h35, de forma híbrida (presencial e online). O curso possui carga horária de 42h e abordará a parte conceitual e prática do cálculo variacional, resolvendo distintas aplicações na física e matemática. As inscrições podem ser feitas via Sigaa na aba de Extensão > Inscrição on-line em Ações de Extensão.
O cálculo variacional é uma ferramenta matemática poderosa, que possui aplicações na física teórica, na matemática e nas diversas engenharias. O professor Hector Salazar, coordenador do minicurso, conta que existe uma noção por parte de alguns estudantes de engenharia que a única forma de resolver problemas da dinâmica clássica é utilizando as leis de Newton. Entretanto, existem outros dois formalismos que são baseados no cálculo variacional: o Lagrangeano e o Hamiltoniano.
As teorias físicas alternativas às baseadas nas leis de Newton, foram propostas com ajuda do cálculo variacional. No formalismo lagrangeano da mecânica clássica, a segunda lei de Newton, por exemplo, pode ser deduzida por meio da equação de Euler-Lagrange a partir de um princípio mais geral da natureza denominado “princípio da mínima ação”. Na matemática, o cálculo variacional também é importante, por exemplo, para estudar as superfícies mínimas e as chamadas curvas geodésicas.
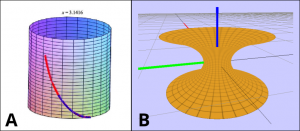
Imagem (A) temos a tautócrona, curva especial no cilindro. Em (B), temos a representação de uma superfície chamada de catenóide.
O professor Salazar cita dois exemplos que podem ser estudados a partir do Cálculo Variacional e que são abordadas no curso. Um deles é a tautócrona (figura A). Nesse tipo de curva, ao soltarmos duas partículas de posições diferentes, partindo do repouso, as partículas chegarão à parte mais baixa no mesmo instante. Já no outro exemplo, a catenóide (figura B), representa a superfície de revolução de área mínima gerada por uma curva plana. Uma aproximação dessa superfície mínima pode ser observada na espuma formada entre dois aros de metal, próximos e lado a lado, após mergulhados em espuma de sabão.
A oficina é ideal para os alunos que pretendem estudar métodos de otimização, com aplicação na pesquisa teórica e prática das engenharias, mecânica teórica ou mecânica clássica (alunos de física). Os requisitos para se matricular são: Alunos que estejam cursando ou tenham cursado Física 2, Cálculo 2 e Álgebra Linear. O professor conta que tem uma boa expectativa para o minicurso e espera realizar algumas publicações à nível de ensino de física com os alunos.
Para mais informações, podem entrar em contato com o professor Hector através do email hectors@ect.ufrn.br


